Aşağıdaki soruyu Martin Gardner'ın Mathematical Circus adlı kitabının 62. ve 63. sayfalarında gördüm.
Çözümü üçgenlerin benzerliğinden yapılan ve kökeni tam olarak bilinmeyen adı çıkmış klasik bulmacalardan birisi hakkında Dudley F. Church şöyle diyor:Problemin büyüsü ilk bakışta sadeymiş gibi görünüp daha sonra kolayca cebirsel bir kargaşaya dönüşen çözümünde yatıyor.Problem uzunlukları farklı iki merdiven hakkında. (Merdivenlerin uzunlukları eşitse, o zaman çözüm bariz oluyor.) Merdivenler şekilde gösterildiği gibi iki binaya yaslanmışlar. Merdivenlerin uzunlukları ve kesişim noktalarının yerden yüksekliği veriliyor. Binalar arasındaki mesafe nedir?
 Gardner kitabında problemin nasıl çözüldüğünü anlatmamış. Sadece dördüncü dereceden bir (kuartik) denklemin çözümüne kadar indirgendiğini not etmiş ve orada bırakmış. Biz ilk önce Gardner'ın kitabında verilen cebirsel denklemi türeteceğiz. Daha sonra o cebirsel denklemin bizzat kendisini de başka bir zaman çalışacağız.
Gardner kitabında problemin nasıl çözüldüğünü anlatmamış. Sadece dördüncü dereceden bir (kuartik) denklemin çözümüne kadar indirgendiğini not etmiş ve orada bırakmış. Biz ilk önce Gardner'ın kitabında verilen cebirsel denklemi türeteceğiz. Daha sonra o cebirsel denklemin bizzat kendisini de başka bir zaman çalışacağız.
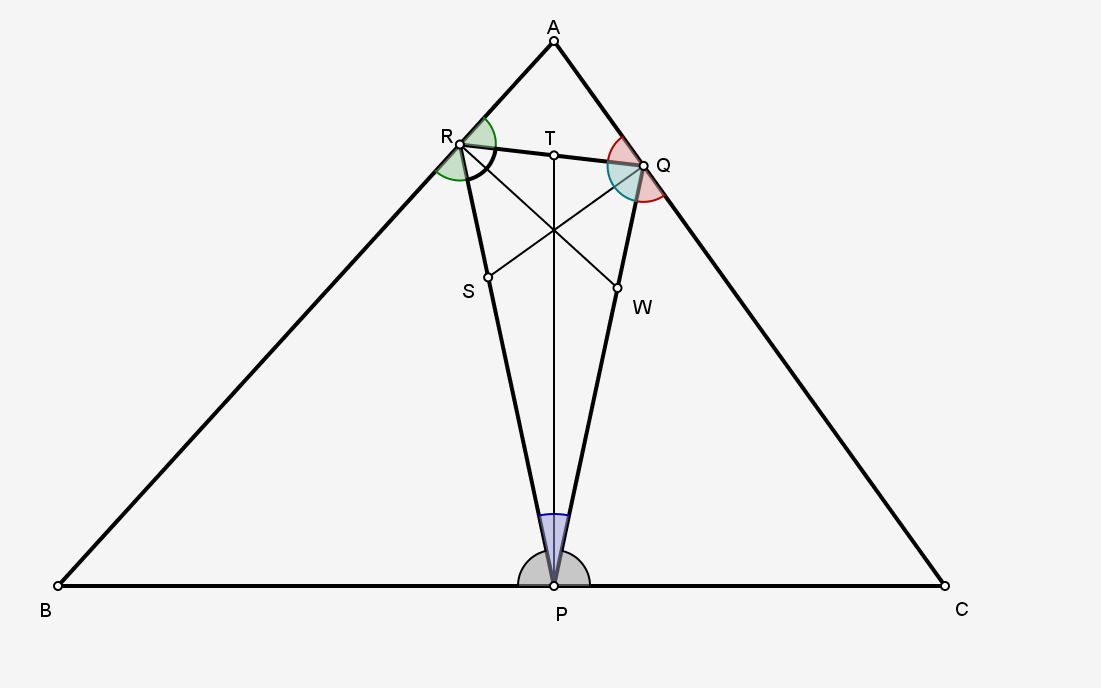
Şekilde kırmızı renkle gösterilen merdivenlerin uzunlukları $|AD|=:a$ ve $|BC|=:b$ olarak veriliyor. Çaprazlama duran merdivenlerin kesişim noktaları $E$ olup, bu noktanın sokağa izdüşümü $F$'tir. Yine soruda $|EF|=:c$ olarak verilmiş. Bunlar problemi çözmede kullanmamıza izin verilen bilinenler. Soruyu çözmek için $|AB|=:h$, $|CD|=:k$, $|BF|=:v$ ve $|FD|=:u$ olmak üzere toplamda dört tane bilinmeyen tanımlayacağız. Her ne kadar bizden $u+v$ uzunluğu istense de, biz bütün bilinmeyenleri $k$ cinsinden ifade edip, daha sonra çözüldüğünden $k$ değerini veren bir denkleme kadar problemi çalışacağız. Genelliği bozmadan $a > b$ kabul edelim.
İlk önce $\triangle ABC$ ve $\triangle BCD$ için Pisagor teoremini uygulayalım. \begin{eqnarray} a^{2} &=& h^{2} + (u+v)^{2} \\ b^{2} &=& k^{2} + (u+v)^{2} \end{eqnarray} Daha sonra da sırasıyle $\triangle DEF \sim \triangle ABD$ ve $\triangle BEF \sim \triangle BCD$ benzerliklerinden iki denklem daha üretebiliyoruz. \begin{eqnarray} \frac{c}{u} &=& \frac{h}{u+v} \\ \frac{c}{v} &=& \frac{k}{u+v} \end{eqnarray} Eleme yöntemlerini kullanarak her bilinmeyeni $k$ cinsiden ifade etmeye çalışacağız. Öncelikle (1) ve (2) nolu denklemleri taraf tarafa çıkarıp yeniden düzenlediğimizde \begin{equation} \bbox[5px,border:2px solid red]{h = \sqrt{a^{2}-b^{2}+k^{2}}} \end{equation} ilişkisini elde ediyoruz. (3) ve (4) nolu denklemleri taraf tarafa böldüğümüzde $u/v = k/h$ ya da \begin{equation} u = \frac{k}{h}v \end{equation} arasonucu karşımıza çıkıyor. Şimdi (2) nolu denklemden de \begin{equation} u = \sqrt{b^{2}-k^{2}} - v \end{equation} arasonucunu gözlersek, o zaman son iki denklemi birbirine eşitlediğimizde ve nihayet (5) nolu denklemi de kullandığımızda \begin{equation} \frac{k}{h}v = \sqrt{b^{2}-k^{2}} - v \ \ \ \Rightarrow \ \ \ \bbox[5px,border:2px solid red]{v = \frac{\sqrt{a^{2}-b^{2}+k^{2}}\sqrt{b^{2}-k^{2}}}{\sqrt{a^{2}-b^{2}+k^{2}}+k}} . \end{equation} Son olarak (8) nolu sonucu (6) nolu denklemde kullanırsak, o zaman bütün bilinmeyenlerin $k$ cinsinden ifade edilmesi süreci bitmiş oluyor. \begin{equation} \bbox[5px,border:2px solid red]{u = \frac{k\sqrt{b^{2}-k^{2}}}{\sqrt{a^{2}-b^{2}+k^{2}}+k}} \end{equation}
İşin nisbeten kolay kısmı bitti. Şimdi bilinmeyen olarak sadece $k$ niceliğini içeren bir denklem bulmamız gerekiyor. Ne yazık ki ilk dört denklemi kullandık. Bu yüzden onlara geri döndüğümüzde totolojik (ve can sıkıcı) sonuçlarla karşılaşabiliriz. Bu yüzden yeni bir denklemle işe başlamamız gerekiyor. Çalıştığımız problemin konfigurasyonundan yola çıkılarak pek çok benzerlik denklemi üretilebilir. Mesela $BEF$ ve $BCD$ üçgenlerinde benzerliği uyguladığımızda \begin{equation} \frac{\sqrt{c^{2}+v^{2}}}{c} = \frac{b}{k} \ \ \ \Rightarrow \ \ \ (c^{2}+v^{2})k^{2} = b^{2}c^{2} \end{equation} denklemi karşımıza çıkıyor. Artık bundan sonra (8) nolu denklemi yukarıda kullanmamız gerekiyor. \begin{equation} \left(c^{2}+\frac{(a^{2}-b^{2}+k^{2})(b^{2}-k^{2})}{a^{2}-b^{2}+2k^{2}+2k\sqrt{a^{2}-b^{2}+k^{2}}}\right) k^{2} = b^{2}c^{2} \end{equation} Amacımıza neredeyse ulaştık! Bu denklem sadece bir tane bilinmeyen içeriyor. Öte yandan Gardner'ın sözünü ettiği cebirsel kargaşa kendini göstermeye başladı. Bundan sonra yapılması gereken manipulasyonları eğer kalem kağıtla yapmaya çalışırsanız çok büyük bir ihtimalle hataya düşersiniz. Bu yüzden Maxima veya open-axiom gibi bir bilgisayar cebir sistemi/yazılımı (Computer Algebra System) kullanmanızı şiddetle tavsiye ediyorum. (Ben Maxima kullandım.) (11) nolu denklem üzerinde yapılması gereken işlemler sırasıyla şöyledir: (a) Önce parantezler açılır ve paydalar eşitlenerek, denklem kesirli ifadelerden temizlenir. (b) Ardından köklü ifadeler bir tarafta, diğer ifadeler öteki tarafta duracak şekilde denklem yeniden düzenlenir. (c) Her iki tarafın karesi alınarak denklem köklü ifadelerden de temizlenir. (Bu aşamada karşılaşılan ifade $k$ bilinmeyenine göre 8. derecedendir. Şaka gibi!) (d) Nihayet $f(k) =0$ formuna getirdiğimiz denklem -eğer çarpanlarına ayrılıyorsa!- çarpanlarına ayrılır. Neyseki şansımız yaver gitti ve 8. dereceden denklemimiz $f(k)=g(k)j(k)$ şeklinde iki tane dördüncü dereceden polinomun çarpımı şeklinde çarpanlarına ayrıldı. Maxima'nın verdiği sonuç aşağıdaki gibidir. \begin{eqnarray} g(k) &=& k^{4} - 2ck^{3} + (a^{2}-b^{2})k^{2} - 2(a^{2}-b^{2})ck + (a^{2}-b^{2})c^{2} \\ j(k) &=& k^{4} + 2ck^{3} + (a^{2}-b^{2})k^{2} + 2(a^{2}-b^{2})ck + (a^{2}-b^{2})c^{2} \end{eqnarray}
Sorun şu: aradığımız $k$ değerini ya $g(k)=0$ ya da $j(k)=0$ denklemini çözerek bulacağız. Bir seçim yapmamız gerekiyor. Şimdi çalıştığımız problemin konfigürasyonu gereği $a^{2}-b^{2} > 0$ olduğundan, $j(k)$ polinomunun bütün katsayıları pozitiftir. O zaman $k>0$ için $j(k)>0$ olacağından, bu polinomun pozitif bir kökü olamaz. Sekiz alternatiften dördünü böylece elemiş oluyoruz. Geriye $g(k)=0$ denklemini çalışmak kalıyor. Gardner'ın kitabında ispatsız yer verdiği denklem de bu.
Bir sonraki gönderimizde $g(k)=0$ denkleminin kök tasnifine derinlemesine bakacağız.