Ortik üçgenin optik özelliği

Problem 6: Dar açılı bir $\triangle ABC$'de $P \in BC$, $Q \in AC$ ve $R \in AB$ olacak şekilde $P$, $Q$ ve $R$ noktaları seçiliyor. $\triangle PQR$'nin çevresinin minimal olması için $P$, $Q$ ve $R$ noktaları nasıl seçilmelidir?

Cevabımız bir kaç aşamadan oluşacak. Öncelikle $m(\angle BPR) = m(\angle CPQ)$, $m(\angle CQP) = m(\angle RQA)$ ve $m(\angle ARQ) = m(\angle BRP)$ olduğunu göstereceğiz. Dikkatli okur bu konfigürasyonun aslında geometrik optikteki yansıma kanunundan başka bir şey olmadığını gözleyecektir. Üçgen biçiminde sürtünmesiz bilardo masasındaki esnek çarpışmalarla yansıyan ve periyodik bir yörünge izleyen bilardo topunun da dinamiği yine aynıdır. Şimdi aradığımız üçgenin çevresini

$$\begin{equation*} s := |RP| + |PQ| + |QR| \end{equation*}$$ tanımlayalım. $\triangle PQR$'nin tam tayin edilebilmesi için üç niceliğin verilmesi yeterlidir. Bunları mesela $x:= |BP|$, $y:=|CQ|$ ve $z := |AR|$ şeklinde seçebiliriz. Şimdi kosinus teoremini uygulayalım ve basitçe $\triangle PQR$'nin kenar uzunluklarını bilinmeyenler ($x$, $y$, $z$) ve bilinenler ($a:=|BC|$, $b:=|AC|$, $c:=|AB|$, $A:=m(\angle BAC)$, $B:=m(\angle ABC)$, $C:=m(\angle ACB)$) cinsinden ifade edelim. $$\begin{equation*} s := \sqrt{x^{2}+(c-z)^{2}-2x(c-z)\cos B} + \sqrt{y^{2}+(a-x)^{2}-2y(a-x)\cos C} + \sqrt{z^{2}+(b-y)^{2}-2z(b-y)\cos A} \end{equation*}$$ Ekstremum şartı bize üç tane denklem verecektir: $$\begin{equation*} \frac{\partial s}{\partial x} = 0, \ \ \ \frac{\partial s}{\partial y} = 0 \ \ \ {\rm ve} \ \ \ \frac{\partial s}{\partial z} = 0. \end{equation*}$$ Ben bunlardan sadece ilkini çalışıp, diğer ikisinin soruşturulmasını okura bırakacağım. (Takip edilmesi gereken yol aşağıdaki çalışmadan kolayca genelleştirilebilir.) İlk ekstremum şartı, türev alınıp yeniden düzenleme yapıldıktan sonra bize aşağıdaki denklemi verecektir. $$\begin{equation*} \frac{x-(c-z)\cos B}{|RP|} = \frac{(a-x)-y \cos C}{|PQ|} \end{equation*}$$ $R$ ve $Q$ noktalarının $BC$ kenarı üzerine izdüşümlerine sırasıyla $U$ ve $V$ dersek, o zaman yukarıdaki son denklemin aslında temel trigonometrik argumanlar kullanılarak $$\begin{equation*} \frac{|UP|}{|RP|} = \frac{|VP|}{|PQ|} \ \ \ \Rightarrow \ \ \ \cos(m(\angle BPR)) = \cos (m(\angle CPQ)) \ \ \ \Rightarrow \ \ \ \bbox[5px,border:2px solid red]{ m(\angle BPR) = m(\angle CPQ)} \end{equation*}$$ sonucunu doğurduğu görülür. Tamamen benzer yöntemlerle $m(\angle CQP) = m(\angle RQA)$ ve $m(\angle ARQ) = m(\angle BRP)$ olduğunu okur gösterebilir.

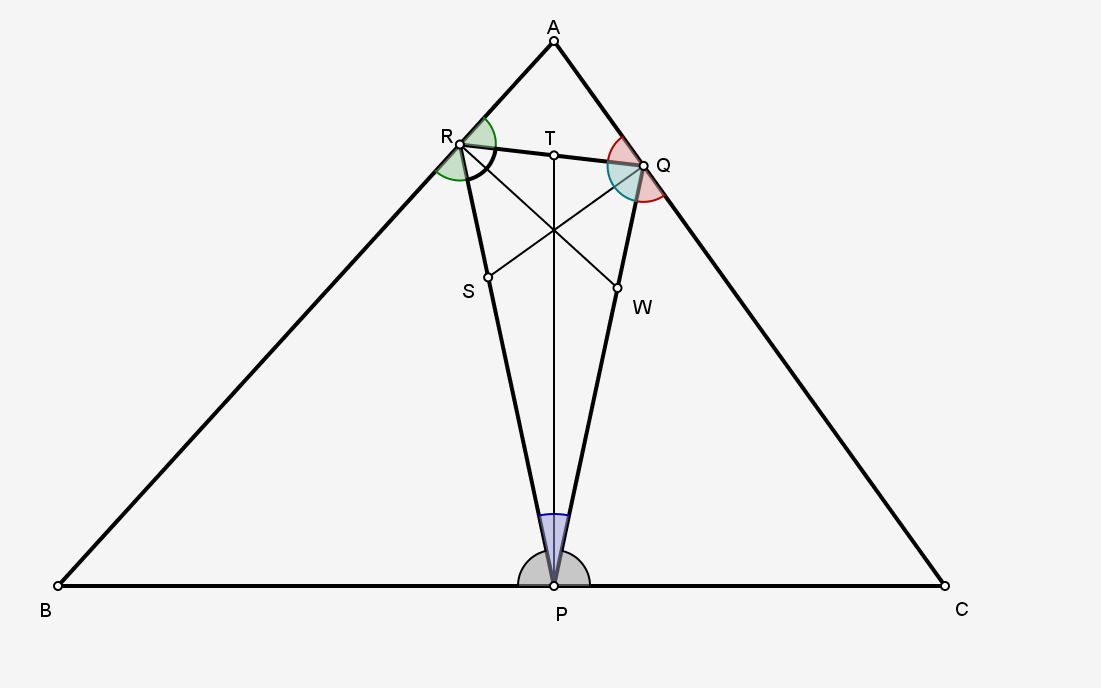İspatımızın ikinci aşamasında $\triangle PQR$'nin iç açı ortaylarını çalışacağız. Hesaplamalarımızda kolaylık olması için

$$\begin{eqnarray} \nonumber \alpha &:=& m(\angle BPR) = m(\angle CPQ), \\ \nonumber \alpha^{\prime} &:=& m(\angle RPT) = m(\angle TPQ), \\ \nonumber \beta &:=& m(\angle CQP) = m(\angle AQR), \\ \nonumber \beta^{\prime} &:=& m(\angle RQS) = m(\angle PQS), \\ \nonumber \gamma &:=& m(\angle BRP) = m(\angle ARQ), \\ \nonumber \gamma^{\prime} &:=& m(\angle QRW) = m (\angle PRW) \end{eqnarray}$$ tanımlayalım. Yansıma kanunundan da kolayca görüleceği üzere $\alpha+\alpha^{\prime} = \beta + \beta^{\prime} = \gamma + \gamma^{\prime} = 90^{\rm o}$ olmalıdır. Yine barizdir ki $\triangle PQR$'nin iç açılarının toplamından ve açı ortay özelliğinden $\alpha^{\prime} + \beta^{\prime} + \gamma^{\prime} = 90^{\rm o}$ olur. Öncelikle $BPTR$ dörtgeninde iç açıların toplamına bakalım. $$\begin{equation*} 360^{\rm o} = B + 90^{\rm o} + \alpha^{\prime} + 2 \beta^{\prime} + 90^{\rm o} + \gamma^{\prime} \end{equation*}$$ ya da $B+\beta^{\prime} =90^{\rm o}$ olacaktır. Bu ise $\bbox[2px,border:2px solid red]{\beta = B}$ sonucunu gerektirir. Okur az önce uyguladığımız tekniği sırasıyla $CPSQ$ ve $ARWQ$ dörtgenlerine uygulayarak $\gamma = C$ ve $\alpha = A$ sonuçlarına da varabilir. Demek ki aradığımız $P$, $Q$, ve $R$ noktaları $\triangle ABC$'ni üç tane benzer (ama genelde birbirine eşit olmayan) üçgene bölüyormuş.

İspatımızın artık son aşamasına geldik. Açı-açı-açı benzerliğinden üç defa faydalanacağız. Öncelikle $\triangle PBR \sim \triangle ABC$ benzerliğinden

$$\begin{equation*} \frac{c-z}{x} = \frac{a}{c} \ \Rightarrow \ z = c - \frac{a}{c}x \ \ \ ... \ \ \ (☿) \end{equation*}$$ denklemini elde ediyoruz. Devamla $\triangle PQC \sim \triangle ABC$ benzerliğinden faydalanarak $$\begin{equation*} \frac{y}{a-x} = \frac{a}{b} \ \Rightarrow \ y = \frac{a^{2}}{b} - \frac{a}{b}x \ \ \ ... \ \ \ (♀) \end{equation*}$$ sonucuna ulaşıyoruz. Son olarak $\triangle AQR \sim \triangle ABC$ benzerliğini de kullanırsak, o zaman $$\begin{equation*} \frac{z}{b-y} = \frac{b}{c} \ \Rightarrow \ z = \frac{b^{2}}{c} - \frac{b}{c}y \ \ \ ... \ \ \ (♁) \end{equation*}$$ sonucuna da ulaşırız. Şimdi (♀) etiketli denklemi (♁) etiketli denklemde kullanalım ve $z$ uzunluğunu $x$ cinsinden verelim. $$\begin{equation*} z = \frac{b^{2}}{c} - \frac{a^{2}}{c} + \frac{ax}{c} \ \ \ ... \ \ \ (♂) \end{equation*}$$ Ama hem (☿) hem de (♂) etiketli denklemler $z$ niceliğini $x$ uzunluğu cinsinden ifade ediyorlar. Bu ikisi birbirine eşit olmak zorundadır. O zaman $$\begin{equation*} c - \frac{a}{c}x = \frac{b^{2}}{c} - \frac{a^{2}}{c} + \frac{ax}{c} \ \Rightarrow \ x = \frac{a^{2}+c^{2}-b^{2}}{2a} \ \ \ ... \ \ \ (♃) \end{equation*}$$ olması gerektiği ortaya çıkar. Kosinus teoremine göre $\cos \beta = (a^{2}+c^{2}-b^{2})/2ac$ olduğundan, biz (♃) etiketli sonucu $x=c \cos \beta$ şeklinde yeniden düzenleyebiliriz. Böylece $\bbox[2px,border:2px solid red]{AP \perp BC}$ olduğunu da kanıtlamış oluyoruz. Okur benzer yöntemlerle $BQ \perp AC$ ve $CR \perp AB$ olduğunu da ispatlayabilir.

Toparladığımızda $P$, $Q$ ve $R$ noktaları, $\triangle ABC$'nin yüksekliklerinin ayaklarıdır. $\triangle PQR$'ne literatürde ortik üçgen denir.