The ingenious method of Rüchhardt (1929) determines the ratio of heat capacities of an ideal gas through elementary mechanics as an alternative to the well established methods of thermal physics. One can find the description of the method elsewhere on the net as well as in Zemansky's influential Heat and Thermodynamics. I was not satisfied by the exposition of the method in Zemansky and decided to present it in my own way.
Adiabats
The method relies neither the first nor the second laws of thermodynamics. We start with The Doctrine of Latent and Specific Heats which states that the instant heating of a thermodynamic system can be described by the following equation. \begin{equation} h(t) := \Lambda_{V}(T(t),V(t)) \dot{V}(t) + C_{V}(T(t),V(t)) \dot{T}(t) \label{doctrine} \end{equation} Here $\dot{x}(t)$ signifies the time derivative of $x(t)$, $\Lambda_{V}(T,V)$ is the latent heat function of the material, and the positive definite function $C_{V}(T,V)$ is the specific heat at constant volume. $t$, as always signifies time. All physical theories rely on the existence of an entity called state and in thermodynamics we assume that the state of a closed sytem can be described by two independent variables, say temperature and volume. The collection of all states is given by the set $\Sigma$ and we assume that $\Sigma$ is simply connected. A thermodynamic process can be represented by a (piecewise) differentiable curve in $\Sigma$. Thus the time parametric function $\mathbf{\alpha} : [a,b] \to \Sigma$ gives all the points $(T(t),V(t))$ of the path traced by a thermodynamic process as time runs from $a$ to $b$.
Among all processes, adiabatic ones stand out for two reasons: They are indispensible in the description of Carnot's heat engine as well as the experiments of Joule which ultimately gave us the second and first laws of thermodynamics, respectively. A process is adiabatic if, and only if, the instant heating function vanishes at all times. Set $h(t)=0$ and rearrange (\ref{doctrine}) to read \begin{equation} \frac{{\rm d}\psi(V)}{{\rm d}V} = -\frac{\Lambda_{V}(\psi(V),V)}{C_{V}(\psi(V),V)}. \label{adiabat} \end{equation} The solutions of the initial value problem (\ref{adiabat}) are called adiabats, they are signified by $T = \psi(V)$, and satisfy the initial condition $T_{\circ} = \psi(V_{\circ})$. The uniqueness of the solutions of ordinary differential equations guarantee that two adiabats either agree on all points in $\Sigma$ or they never cross.
A second hidden postulate of the founding fathers of thermodynamics was their relience on the existence of a pressure function $p=\varpi(T,V)$ that gives the equilibrium pressure of a material in state $(T,V)$. Pressure function is further assumed to satisfy the mechanical stability condition expressed by $\tfrac{\partial \varpi}{\partial V} < 0$. One can invert the functional relation $p=\varpi(T,V)$ to solve for volume $V=\varphi(T,p)$ and feed this to Eq. (\ref{doctrine}) to arrive at \begin{eqnarray}\nonumber h&=&\Lambda_{V}(T,V)\left\{ \frac{\partial V}{\partial T}\dot{T}+\frac{\partial V}{\partial p}\dot{p}\right\} + C_{V}(T,V)\dot{T}\\ \nonumber &=& \Lambda_{V}(T,V)\frac{\partial V}{\partial p}\dot{p} + \left\{ \Lambda_{V}(T,V)\frac{\partial V}{\partial T} + C_{V}(T,V)\right\} \dot{T} \\ &=:& \Lambda_{p}(T,V) \dot{p} + C_{p}(T,V) \dot{T} \end{eqnarray} where the specific heat at constant pressure is $C_{p}(T,V):=C_{V}(T,V)+\Lambda_{V}(T,V)\tfrac{\partial V}{\partial T}$ and $\Lambda_{p}$ is analogously defined. Obviously, if one plugs in $V=\varphi(T,p)$ to these relations then everything can be transformed to $Tp$ space.
A quantity that is of much interest to the studies of thermodynamics and fluid mechanics is the ratio of two heat capacities, $\gamma := C_{p}/C_{V}$. Clearly $\gamma = 1 + \tfrac{\Lambda_{V}}{C_{V}} \tfrac{\partial V}{\partial T}$. This can be exploited in Eq. (\ref{adiabat}) to read \begin{equation} \frac{{\rm d}\psi(V)}{{\rm d}V} = -(\gamma (\psi(V),V)-1) \frac{\partial T}{\partial V} (\psi(V),V) . \label{adiabat2} \end{equation} This equation is exact in the sense that it only postulates the validity of The Doctrine of Latent and Specific Heats and the existence of a pressure function of a mechanically stable material. Now we are in a position to state a bold and simplifying assumption which requires $\gamma$ to be a constant for an ideal gas. This adscititious hypothesis must be supported by experimental evidence and measurements suggest that for monatomic gases $\gamma \approx 5/3$. Since we are also working with an ideal gas fluid $\varpi(T,V) := K T/V$ where $K$ is a positive constant. Then $\tfrac{\partial T}{\partial V} = p/K = T/V$. Substitute this to Eq. (\ref{adiabat2}) to read \begin{equation} \frac{{\rm d}\psi(V)}{{\rm d}V} = -(\gamma -1) \frac{\psi(V)}{V} . \label{adiabatideal} \end{equation} Solution of (\ref{adiabatideal}) is an elementary exercise of calculus and left to the reader. It is \begin{equation} T = \psi(V) = \frac{T_{\circ}V^{\gamma-1}_{\circ}}{V^{\gamma-1}} \end{equation} By substituting $T = pV/K$ for an ideal gas one can represent the adiabat in $pV$ space more succinctly as \begin{equation} pV^{\gamma} = p_{\circ}V_{\circ}^{\gamma}. \label{adiabatcurve} \end{equation}
Rüchhardt's method
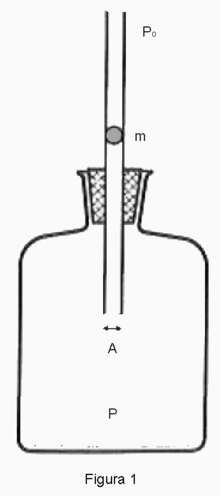 Rüchhardt's method can be described by the figure on the right which is taken from wikipedia. There is a spherical ball of mass $m$ and radius $r$ that just fits the glass pipe which is immersed into the vessel that encloses an ideal gas inside. Rüchhardt's assumptions are as follows: (1) The ball is frictionless and can move up and down in the pipe with no dissipation of its mechanical energy. (2) During the motion of the ball no gas escapes. (3) There is not enough time for the system to thermally equilibrate with its surroundings, ergo the entire process may be regarded as adiabatic if the duration of the experiment is not too long.
Rüchhardt's method can be described by the figure on the right which is taken from wikipedia. There is a spherical ball of mass $m$ and radius $r$ that just fits the glass pipe which is immersed into the vessel that encloses an ideal gas inside. Rüchhardt's assumptions are as follows: (1) The ball is frictionless and can move up and down in the pipe with no dissipation of its mechanical energy. (2) During the motion of the ball no gas escapes. (3) There is not enough time for the system to thermally equilibrate with its surroundings, ergo the entire process may be regarded as adiabatic if the duration of the experiment is not too long.
As a preliminary lemma we start by calculating the total (net) force acting on a half sphere which suffers a constant gas pressure $p$. It is agreed that the north pole of the sphere is aligned in $\mathbf{k}$ direction. We have ${\rm d}{\mathbf F} = -p {\mathbf {\hat{n}}}{\rm d}S$ where ${\rm d}S$ is the area element and $\mathbf{\hat{n}}$ is the unit normal to that area element. For a spherical surface of radius $r$ they are ${\rm d}S := r^{2}\sin \theta {\rm d}\theta {\rm d}\phi$ and $\mathbf{\hat{n}} := \sin \theta \cos \phi \mathbf{i} + \sin \theta \sin \phi \mathbf{j} + \cos \theta \mathbf{k}$. Then the net force acting on the half sphere can be calculated by an elementary exercise of calculus to read \begin{equation*} \mathbf{F} = -pr^{2}\int\limits_{0}^{2\pi}{\rm d}\phi \int\limits_{0}^{\pi/2} {\rm d}\theta \sin \theta \mathbf{\hat{n}} = -p\pi r^{2} \mathbf{k} . \end{equation*} Note that due to the symmetry of the surface, only the vertical component of the net force is non vanishing.
At equilibrium let the internal pressure of the gas be $p_{\rm eq}$ and the atmospheric pressure which is constant throughout the experiment be $p_{\circ}$. Then the condition of mechanical equilibrium reads \begin{equation*} p_{\circ} \pi r^{2} + mg = p_{\rm eq} \pi r^{2} \end{equation*} which says that the pressure inside the vessel is slightly larger than the atmospheric pressure. Let the volume of the gas at equilibrium be $V_{\rm eq}$. If one moves the ball from equilibrium by a distance $z$, then the volume of the gas becomes $V = V_{\circ} + z \pi r^{2}$. Consequently, by the assumption of adiabaticity the gas pressure must change into \begin{equation*} p = p_{\rm eq}\frac{V^{\gamma}_{\rm eq}}{(V_{\rm eq} + z \pi r^{2})^{\gamma}} \approx p_{\rm eq} \left( 1 - \frac{z\pi r^{2}}{V_{\rm eq}}\right)^{\gamma} \approx p_{\rm eq} \left( 1-\gamma\frac{z\pi r^{2}}{V_{\rm eq}}\right) \end{equation*} where the assumption of small deviations $z\pi r^{2}/V_{\rm eq} \ll 1$ and application of well known Neuman series and Taylor approximations are used to linearize the pressure of the gas.
Upon the displacement of the ball the net force acting on it can be linearized accordingly. \begin{equation*} \mathbf{F}_{\rm net} = (p\pi r^{2} - mg - p_{\circ}\pi r^{2}) \mathbf{k} \approx p_{\rm eq} \left( 1-\gamma\frac{z\pi r^{2}}{V_{\rm eq}}\right)\pi r^{2}\mathbf{k} - p_{\rm eq} \pi r^{2}\mathbf{k} = -\frac{\gamma p_{\rm eq}\pi^{2} r^{4}}{V_{\rm eq}}z \mathbf{k} \end{equation*} It is time to invoke the second law of motion in the form $\mathbf{a} = \tfrac{1}{m} \mathbf{F}_{\rm net}$ where $\mathbf{a} := \ddot{z} \mathbf{k}$. Then the equation of motion for $z$ is \begin{equation} \ddot{z}(t) \approx -\frac{\gamma p_{\rm eq}\pi^{2} r^{4}}{mV_{\rm eq}}z(t) . \label{sho} \end{equation} Our efforts to linearize the gas pressure pays off and we recognize the equation of motion for a simple harmonic oscillator of natural frequency $\omega$ in Eq. (\ref{sho}) where \begin{equation} \omega :=\sqrt{\frac{\gamma p_{\rm eq} A^{2}}{mV_{\rm eq}}} \label{freq} \end{equation} and the cross section of the glass pipe is substituted as $A := \pi r^{2}$. Let the period of the oscillations be $\tau$. Then the relation $\omega = 2 \pi / \tau$ can be solved for $\gamma$ to read as follows. \begin{equation} \boxed{ \gamma = \frac{4 \pi^{2}mV_{\rm eq}}{p_{\rm eq}A^{2}\tau^{2}} } \label{ruchhardt} \end{equation} This is the Rüchhardt formula to measure $\gamma$ via the measurement of the period of oscillations of the spherical ball $m$.
In the desing of the experiments the laboratory worker needs a $\tau$ that is not too long for otherwise the neglected friction and leakage can become pertinent. Nor a very short $\tau$ makes the detection of a periodic motion feasable with human eye. For the optimal design we should chose the density $d := m/(\tfrac{4}{3}\pi r^{3})$ and the radius of the ball such that $\tau \sim 1$ s or so. Rearrange the Rüchhardt formula to express the period of the motion as \begin{equation} \tau = \sqrt{\frac{16 \pi V_{\rm eq}}{3 p_{\rm eq} \gamma} \frac{d}{r}} . \end{equation} Keep in mind that $\gamma \sim 1$ for almost every material and the apparatus dependence of $\tau$ is given as $(d/r)^{1/2}$. It is up to the designer of the experiment to play with $r,d$, and $V_{\rm eq}$ to bring $\tau$ into a sensible interval. (We do not have much freedom on $p_{\rm eq}$ as it must be very close to the atmospheric pressure.)
Further reading
Present post is obviously influenced by the works of the philomath Clifford A. Truesdell. Owen's textbook is a good source for a beginner of rational thermodynamics. Finally Chapter 5 of Zemansky is where the Rüchhardt method is described in a less quantitative way.
- Clifford A. Truesdell and Subramanyam Bharatha, The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines Rigorously Constructed upon the Foundation Laid by S. Carnot and F. Reech, Springer-Verlag, New York, 1977.
- Dawid R. Owen, A First Course in the Mathematical Foundations of Thermodynamics, Springer-Verlag, New York, 1984.
- Mark W. Zemansky and Richard H. Dittman, Heat and Thermodynamics, McGraw-Hill, New York, 1996. 7th edition.
Hiç yorum yok:
Yorum Gönder